 Discrete Gaussian distribution
Discrete Gaussian distribution
In the lattice-based encryption scheme using Learning-With-Errors (LWE), the error or noise vector is created by sampling a Discrete Gaussian Distribution. This page looks at how this works.
Gaussian or normal distribution | Discrete Gaussian distribution | Discrete Gaussian distribution over $\mathbb{Z}_q$ | Discrete Gaussian distribution with width σ = 3.0 | Availability in Sage | Implementation in Python | Rate this page | Contact us
Gaussian or normal distribution
About 68% of values drawn from a normal distribution are within one standard deviation σ away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations.So if we sampled 100 values from a Gaussian distribution with $\sigma = 1.0$, we would have 100 real numbers and would expect approximately 68 of these 100 samples to lie between $-1$ and $+1$, approximately 14 to lie between $+1$ and $+2$, and about 2 to lie between $-2$ and $-3$. You can guarantee with overwhelming odds not to get any values greater than $\pm 6$.
Discrete Gaussian distribution
When we sample a discrete distribution with mean $\mu=0$, the output is a set of integers, centered on zero. This is best explained with a diagram. Here is a histogram plot (shown in blue) of values sampled from a discrete Gaussian distribution with $\sigma=1.0$. The y-axis shows the fraction of the total. The line in red is the probability density function for the Gaussian distribution over the reals.
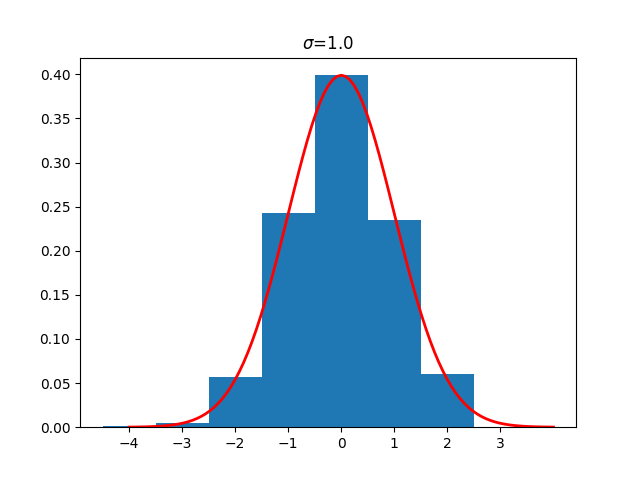
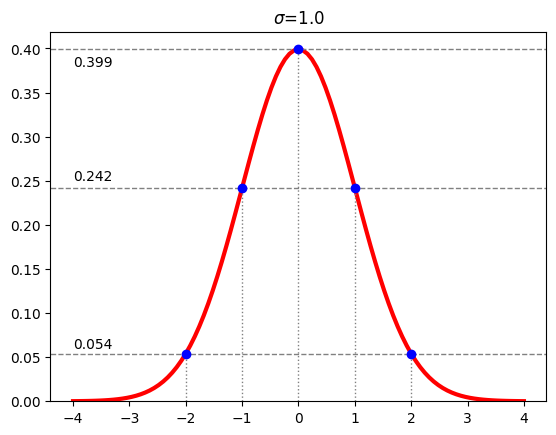
Note that the width of one standard deviation is one integer unit. (You may see such a discrete distribution described as having a width of one.) Note that about 40% of the results are equal to zero, about 24% are equal to $+1$ or $-1$, and about 5% are equal to $+2$ or $-2$. Compare these numbers to the blue dots in the diagram over the reals below.
Discrete Gaussian distribution over $\mathbb{Z}_q$
The effect becomes clearer if we look at the same sample over the finite field $\mathbb{Z}_{31}$
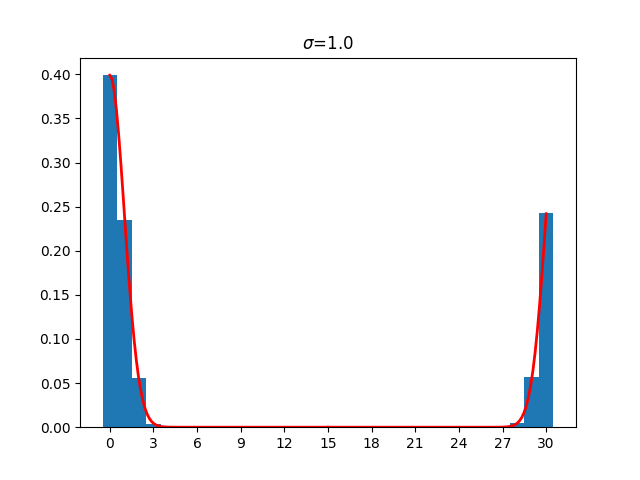
Note how the results bunch up at either end and note the virtually zero probability of values between 4 and 27 ($q-4$).
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 29, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30]
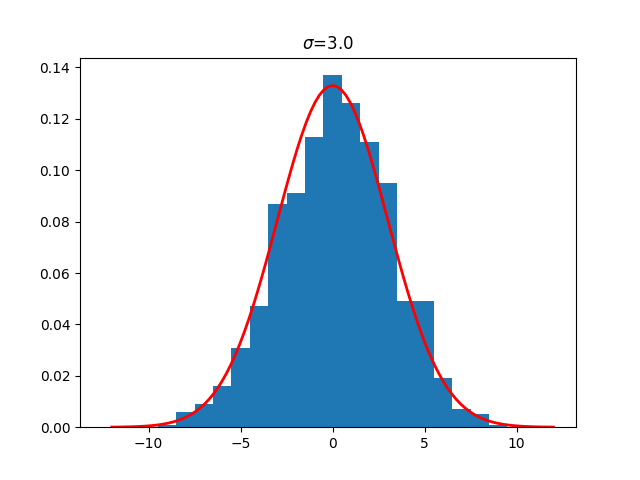
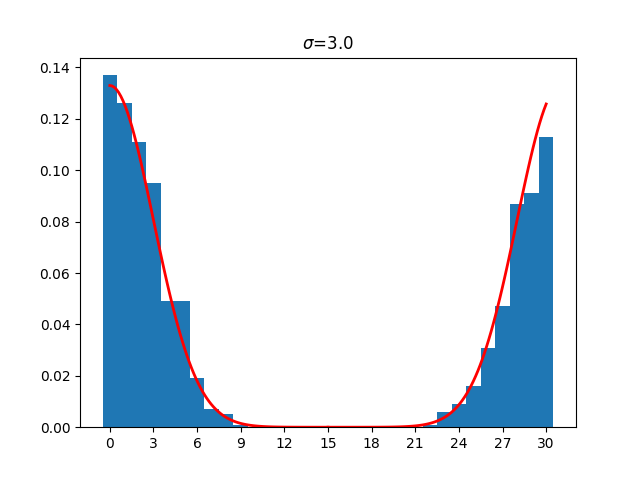
Discrete Gaussian distribution with width $\sigma=3.0$
For comparison, consider a sample of a discrete Gaussian distribution with width $\sigma=3.0$. With a larger $\sigma$ the curve is flatter, the probability values in the y-axis are reduced by a factor of three, and the width of a standard deviation is three bars of width one.
Availability in Sage
See DiscreteGaussianDistributionIntegerSampler Discrete Gaussian Samplers over the Integers in the Sage Reference Manual.
import sage.stats.distributions.discrete_gaussian_integer as dgi def sample_noise(N, R): D = dgi.DiscreteGaussianDistributionIntegerSampler(sigma=1.0) return vector([R(D()) for i in range(N)]) R = Integers(q) e = sample_noise(N, R)
Implementation in Python
|
|
discrete_gaussian_zq.py | Library source code |
import discrete_gaussian_zq as Dgi dgi = Dgi(q) e = [dgi.D() for x in range(N)]
Example in field $\mathbb{Z}_{31}$
dgi = Dgi(31)
e1 = [dgi.D() for x in range(40)]
print("e1 =", e1)
e1 = [1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 30, 1, 0, 30, 1, 0, 1, 0, 1, 29, 30, 30, 0, 30, 30, 0, 1, 1, 30, 30, 0, 30, 2, 30, 30, 0, 30, 0, 0, 2]
Rate this page
Contact us
To contact us or comment on this page, please send us a message.
This page first published 25 February 2024. Last updated 9 September 2025

