 Winternitz One-Time Signature (WOTS)
Winternitz One-Time Signature (WOTS)
The Winternitz One-Time Signature (WOTS) was proposed by Winternitz in 1979, shortly before the publication of Lamport's paper. It is described by Merkle [MER79].
Winternitz improvement (WOTS)
Winternitz parameter
A problem with Winternitz
Adding a checksum to WOTS
WOTS+
Winternitz improvement (WOTS)
-
Have a secret key $x$ and apply $H$ repeatedly $w$ times to form the public key, for example $pk = H^{w}(x)$ where $w=16$.
- where $H^w = H(H(H(\cdots(H(x))))$ denotes $H$ applied $w$ times. We call this a hash chain.
- This allows us to sign $\log_2(16) = 4$ bits of information instead of just one with a single key value.
- To create a signature, split the message digest to be signed into blocks of 4 bits and interpret each block of 4 bits as an integer in the range $[0,15]$.
- To sign the 4 bit message $1001$ (decimal 9), reveal $H^9(x)$.
- To verify, compute $H^7(H^9(x)) = H^{16}(x)$ and check this equals the published value of $H^{16}(x)$.
- More generally, given a message integer $m$ in the range $[0,w-1]$, reveal $H^{m}(x)$ as its signature.
- To verify, show that $H^{w-m}(H^{m}(x)) = H^w(x)$.
So, to use a naive Winternitz OTS scheme using SHA-256 with $w=16$, we do the following
- Your private key is $x_0, x_1, x_2, \ldots, x_{63}$
- Your public key is $H^{16}(x_0), H^{16}(x_1), H^{16}(x_2), \ldots, H^{16}(x_{63})$
- Compute a 256-bit digest of the message $M$ to-be-signed, $md = \text{SHA-256}(M)$.
- Split the 256-bit $md$ into 64 four-bit blocks and interpret each block as an index integer $m_i$ in the range $[0,15]$
- $md = m_0, m_1, \ldots m_i, \ldots m_{63}$; $0 \leq m_i < 16$
- For each $m_i$, reveal $H^{m_i}(x)$ as its signature
An example with $w = 16$ and a message digest of 256 bits.
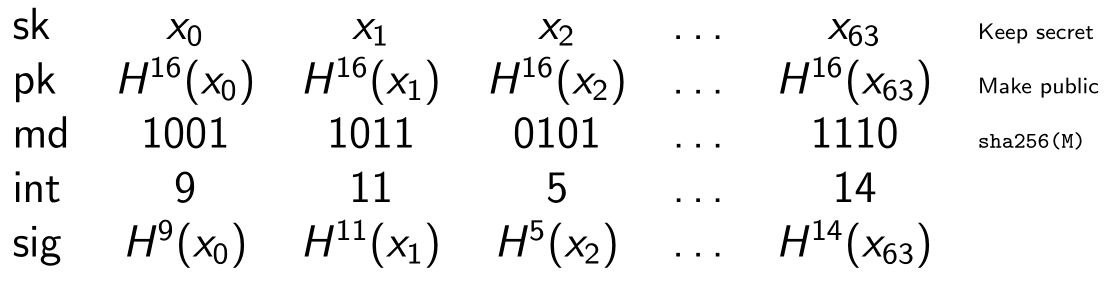
Winternitz parameter
- The value of $w$ is called the Winternitz parameter.
- We don't have to use $w=16$, we can use other convenient powers of two such as 4 or 256.
- $w$ is usually selected from the set $\{4,16,256\}$ giving convenient bit lengths of $\log_2(w)$ $\{2,4,8\}$, respectively.
- be aware that some authors use $w$ to denote the number of bits, so the range of integers becomes $[0, 2^w-1]$.
- Choosing a value for $w$ is a trade off between a shorter signature and increased processing time. Its value has no effect on the security of the scheme.
A problem with Winternitz
- Since $F^9(x)$ is public, an attacker could compute $F^{10}(x)$ and claim that the signed 4-bit message was 1010 (decimal 10) rather than 1001.
- More generally, if an attacker can find a message digest where each index value is greater than the original, they can forge a signature over the new message.
- To fix, we append a checksum to the message digest before signing.
- If the digest has length $n$, the checksum is typically of length of the order $\log_2(n)$.
Adding a checksum to WOTS
Here is a way to compute a checksum, as used in SPHINCS+. For our example above, len_1 = 64 and the length of the checksum is 12 bits.
// Compute checksum for msg of len_1 w-bit integers
csum = 0;
for ( i = 0; i < len_1; i++ ) {
csum = csum + w - 1 - msg[i];
}
- The checksum is converted to a bit string of length 12 bits, split into 3 x 4-bit blocks to give 3 more index integers, which are appended to the 64 integers from the message digest.
- The signature is now computed over these 67 integers instead of 64. Note that we now need a key of 67 values.
- Remember that a forgery is only possible if we can find a new message digest with every index value greater than the original.
- The checksum computed here ensures that if such a message digest exists, then the checksum will produce at least one index less than the original, which cannot be forged.
- We will see an example of this later when we compute the The Hyper Tree Signature.
WOTS+
WOTS+ is an improvement over WOTS designed to prevent certain attacks. [WOTSPLUS]
The idea is that instead of just using the plain hash function $H$ each time in the hash chain, a different chaining function is used every time derived from a "family" of keyed hash functions. By family of hash functions it means use a keyed hash function with a "tweak". This ensures domain separation between each member of the hash function family.
A tweakable hash function takes public parameters P and context information in form of a tweak T in addition to the message input. The public parameters can be thought of as a function key or index. The tweak can be interpreted as a nonce.
F = H(PUBLICKEY || NONCE || msg[i])
In practice, this just means that the input to the hash function is distinct each time it is called.
In SPHINCS+, the function F is defined as
F(PK.seed, ADRS, X) = Hash(PK.seed || ADRS || X)where
PK.seed is a public seed, ADRS is an address in the virtual tree structure of SPHINCS+, and X is the input string.
In plain WOTS, where $pk=H^w(x)$, we can define a chaining function $C$ recursively as
C[i] = H(C[i-1]), C[0] = X
so $C[w] = H^w(x)$. This uses the same H function for each iteration.
In WOTS+, the chaining function $C$ is defined recursively using the tweakable hash function $F$
C[i] = F(PK.seed, ADRS[i], C[i-1]), C[0] = X
where ADRS[i] includes the counter, $i$.
Domain separation is used to allow the use of the same hash function in different situations (domains). By adding a domain separator that is different each time
(PK.seed||ADRS[i]) you are effectively using a different hash function each time you hash msg which ensures a different result even if msg[i] repeats.
| << previous: One-time signature (OTS) scheme | Contents | next: Merkle Tree >> |
Rate this page
Contact us
To comment on this page or to contact us, please send us a message.
This page first published 17 March 2023. Last updated 9 September 2025.

