Merkle Tree

The concept of a Merkle Tree as a binary authentication tree was introduced in [MER79].

• A Merkle Tree is a binary authentication tree built over a set of $n$ values, $Y_1 \ldots Y_n$.
• These $Y$ may be chunks of data we need to authenticate (perhaps in a Bitcoin chain), or OTS public keys we may want to publish as part of a larger scheme.
• The parent of each leaf $Y_i$ is the hash of that value, $H(Y_i)$.
• Each node in the binary tree is the hash of the values of both its children.
  • node = H(leftchild || rightchild)
• The value of the root node is published as a public authentication value.

Merkle Tree with $n=8$

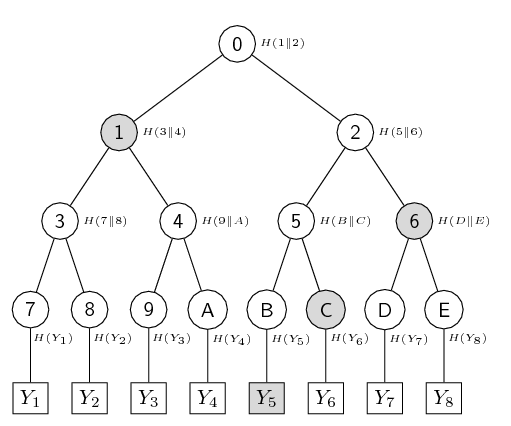
Authenticating the leaf values

• If we know all the values, $Y_1 \ldots Y_n$, we can reconstruct the tree and compare the resulting root value with the published value.
• But this means an end user needs to store all the values, $Y_1 \ldots Y_n$
• What if we just need to verify one value, say $Y_5$?
• To do this we actually only need the values of the nodes at $C$, $6$ and $1$ (shown shaded in the diagram above).
• Along with the value of $Y_5$ we can use these 3 values to compute the root value and compare to the published value.
• We call this an authentication path.
• Note we require the value of exactly one node at each level to do this.
• That means if we have $n$ leaves, the authentication path will consist of $\log_2(n)$ values, e.g. $\log_2(8) = 3$

Example Merkle Tree

• Here is a simple example of a Merkle tree. To make the representation of the tree manageable, we cheat and simplify the hash function so it only outputs a digest value of 4 bytes. This is obviously not secure, but it makes displaying the results less cumbersome, and still shows the underlying concept.

• In this example, we have eight key values, $Y_0,\ldots,Y_7$, each 4 bytes long represented in hexadecimal. (Note index-0 this time)

• The leaf nodes (7-E) contain the 4-byte hash of the keys.

• Each internal node contains the hash of its left and right child node value.

• The authentication path for $Y_4$ is C $\rightarrow$ 6 $\rightarrow$ 1.

• The path from the root to the leaf with index 4 (binary 100) is shown in blue. The index value in binary is interpreted bit-by-bit, going to the left child if the bit is zero and to the right child if the bit is one.

• The authentication path consists of the siblings of the nodes on the path to the leaf.

Calculations for example Merkle tree

Our special "weak" hash function $H$ is defined in Python as follows. (Note that the hash digests are computed over the decoded binary values of the hex strings.)

import hashlib
def H(val: str) -> str:
    """Weak hash function returning hex-encoded 4-byte hash."""
    return hashlib.sha256(bytes.fromhex(val)).hexdigest()[:8]

Some sample calculations.

B = H(Y_4) = H(f7d5e02e) = 59bb626f
5 = H(B||C) 
  = H(59bb626f || 804c9bdb) = 7890c8b6
2 = H(5||6)
  = H(7890c8b6 || e090b2ce) = 009a4350
root, 0 = H(1||2) 
  = H(076f83f6 || 009a4350) = 03583268

• The authentication path for leaf $Y_4=\texttt{f7d5e02e}$ is
  • $C = \texttt{804c9bdb}$
  • $6 = \texttt{e090b2ce}$
  • $1 = \texttt{076f83f6}$
• The path can be verified by showing that
  • $H(1 \parallel H(H(H(Y_4)\parallel C) \| 6)) = \text{root}$
  • There is a neat way to do this using binary numbers shown in the Python code below.

Python code

# Required root value in Merkle tree
root = "03583268"
# Authentication path
authpath = [
"804c9bdb",
"e090b2ce",
"076f83f6",
]
print("authpath=", [x for x in authpath])
# Known key value
sk = "f7d5e02e" # Y_4
print(f"key={sk}")

# Compute leaf value above sk
idx = 4  # 0-based index of Y_4
node = H(sk)  # leaf node

for ap in authpath:
    print(f"idx={idx}")
    # Get last bit of child idx
    lastbit = idx & 1
    # Move up to next level
    idx >>= 1
    print(f"child node={node}")
    print(f"authpath={ap}")
    # Last bit of child determines left/right order of authpath
    if (lastbit):
        print(f"m1,m2={ap} {node}") 
        node = H(ap + node)
    else:
        print(f"m1,m2={node} {ap}") 
        node = H(node + ap)
    print(f"node={node}")

print(f"Required root={root}")
assert(root == node)

authpath= ['804c9bdb', 'e090b2ce', '076f83f6']
key=f7d5e02e
idx=4
child node=59bb626f
authpath=804c9bdb
m1,m2=59bb626f 804c9bdb
node=7890c8b6
idx=2
child node=7890c8b6
authpath=e090b2ce
m1,m2=7890c8b6 e090b2ce
node=009a4350
idx=1
child node=009a4350
authpath=076f83f6
m1,m2=076f83f6 009a4350
node=03583268
Required root=03583268

Benefits of using a Merkle Tree

• The issuer can publish a single root value as a "trusted" authentication value for the $n$ leaves.

• The issuer can publish a single leaf value along with its authentication path.

• A verifier can recompute and check that the authentication path results in the "trusted" root value.

A warning about Merkle trees

• See Bitcoin vulnerability (CVE-2012-2459) a vulnerability if the number of hashes in the list at a given level is odd.

• Hint: Merkle trees work most efficiently (and safely) if they are perfect. In a perfect tree, all internal nodes have two children and all leaves are at the same level. A perfect Merkle tree of height $h$ has exactly $2^h$ leaf nodes. This avoids the Bitcoin vulnerability above.
  • Some authors use the word complete, but not all definitions of "complete" mean "perfect" as described above.

Rate this page

Contact us

To comment on this page or to contact us, please send us a message.

This page first published 17 March 2023. Last updated 9 September 2025.