SPHINCS+ Example

We work in detail through an example signature from the SPHINCS+ NIST-PQ round 3 submission dated 1 October 2020.

We use JavaScript to display the mathematics on this page. Please enable JavaScript in your browser for it to work.

`SPHINCS+-SHA2-128f-simple`

For this example we chose the algorithm SPHINCS+-SHA2-128f-simple.

This uses the hash function SHA-256 with 128 bits of security ($n=16$ bytes), using the fast parameters (faster computation, larger signature size), with the simple form (i.e. it does not use a bit mask when hashing^†).

Reference: NIST-PQ-Submission-SPHINCS-20201001\KAT\sphincs-sha256-128f-simple\PQCsignKAT_64.rsp
Test case 0

This is included in the (large) download http://sphincs.org/data/sphincs+-round3-submission-nist.zip (128 MB)

Changes since October 2020

CAUTION: Since the round 3 submission was made in October 2020, a revision v3.1 was submitted in June 2022, which makes security improvements to the SHA-256 implementation. These latest changes are not reflected here. There will most likely be more changes between now and when NIST actually releases the final standard.

Latest update 2023-08-24: see FIPS 205 (Draft) Stateless Hash-Based Digital Signature Standard. This is based on revision v3.1.

In any event, you should get the general idea from these calculations even if the final details are slightly different.

† The alternative to the simple form was robust, which used a bit mask when hashing. The robust variants have been dropped from the NIST standardisation process.

Details

SPHINCS+ public key [2n bytes]

B505D7CFAD1B497499323C8686325E47   # PK.seed
4FDFA42840C84B1DDD0EA5CE46482020   # PK.root
--------------------------------------------
SPHINCS+ private key [4n bytes]

7C9935A0B07694AA0C6D10E4DB6B1ADD   # SK.seed
2FD81A25CCB148032DCD739936737F2D   # SK.prf
B505D7CFAD1B497499323C8686325E47   # PK.seed
4FDFA42840C84B1DDD0EA5CE46482020   # PK.root
--------------------------------------------
Message [33 bytes]

D81C4D8D734FCBFBEADE3D3F8A039FAA
2A2C9957E835AD55B22E75BF57BB556A
C8

The signature is 17088 bytes long.

Example signature in full 1068 lines of 16 bytes. This is just to show how big it is. Really big. You just won’t believe how vastly, hugely, mindbogglingly big it is [ref].

Example signature broken down

Parameters

The parameters for SPHINCS+-SHA2-128f-simple are:

    n = 16  # security parameter in bytes
    w = 16  # Winternitz parameter 
    lg(w) = 4
    h = 66  # hypertree height
    d = 22  # number of layers in hypertree
    k = 33  # number of trees in FORS
    t = 64 = 2^6  # number of leaves in FORS
    a = 6  # height of FORS trees = lg(t)
    h/d = 66/22 = 3  # HT subtree size
    len = len1 + len2 = 32 + 3 = 35

where $\lg(x) \equiv \log_2(x)$, i.e. if $x=2^y$ then $\lg(x)=y$

Quirks when using SHA-256

When using SHA-256, some changes are made to speed up the calculations

The ADRS parameter is compressed from 32 bytes to 22 to reduce the number of calls to the SHA256 block algorithm.
Extra zero-byte padding is added to PK.seed before hashing (BlockPad(PK.seed)) so this value can be pre-computed and called repeatedly.
If an output length $n \lt 32$ bytes is required, just truncate to the first $n$ bytes.

NOTE: there are changes to the SHA-256 implementation in revision v3.1 not reflected here.

The signature components

The signature in this example is of length 17088 bytes and consists of 3 parts:

The Randomizer R of length $n=16$ bytes.
The FORS signature (SIG_FORS) of length 3696 bytes:
```
k * (|fors_sig_sk| + |fors_auth_path|) * n =
k * (1 + a) * n = 33 * (1 + 6) * 16 = 3696
```
where |x| denotes the size of x in blocks of n bytes: |fors_sig_sk|=1, |fors_auth_path|=a=6.
The Hypertree signature (SIG_HT) of length 13376 bytes:
```
d * (|ht_sig| + |ht_auth_path|) * n =
d * (len + (h/d)) * n = 22 * (35 + 3) * 16 = 13376
```
where |ht_sig|=len=35, |ht_auth_path|=h/d=66/22=3.

How many private keys are there?

As an aside, let us consider how many private keys there are.

Here is an example of a small tree from the SPHINCS+ paper and a diagram of one FTS node. The small tree has $h=9$ and $d=3$.

Small WOTS tree

This small tree has $(2^{h/d})^d = (2^3)^3 = 2^9 = 512$ OTS nodes at the bottom HT layer, each able to sign a FORS tree (FTS node). Each FORS tree has $k\times t$ private key values, where $k$ and $t$ are parameters of the FORS tree.

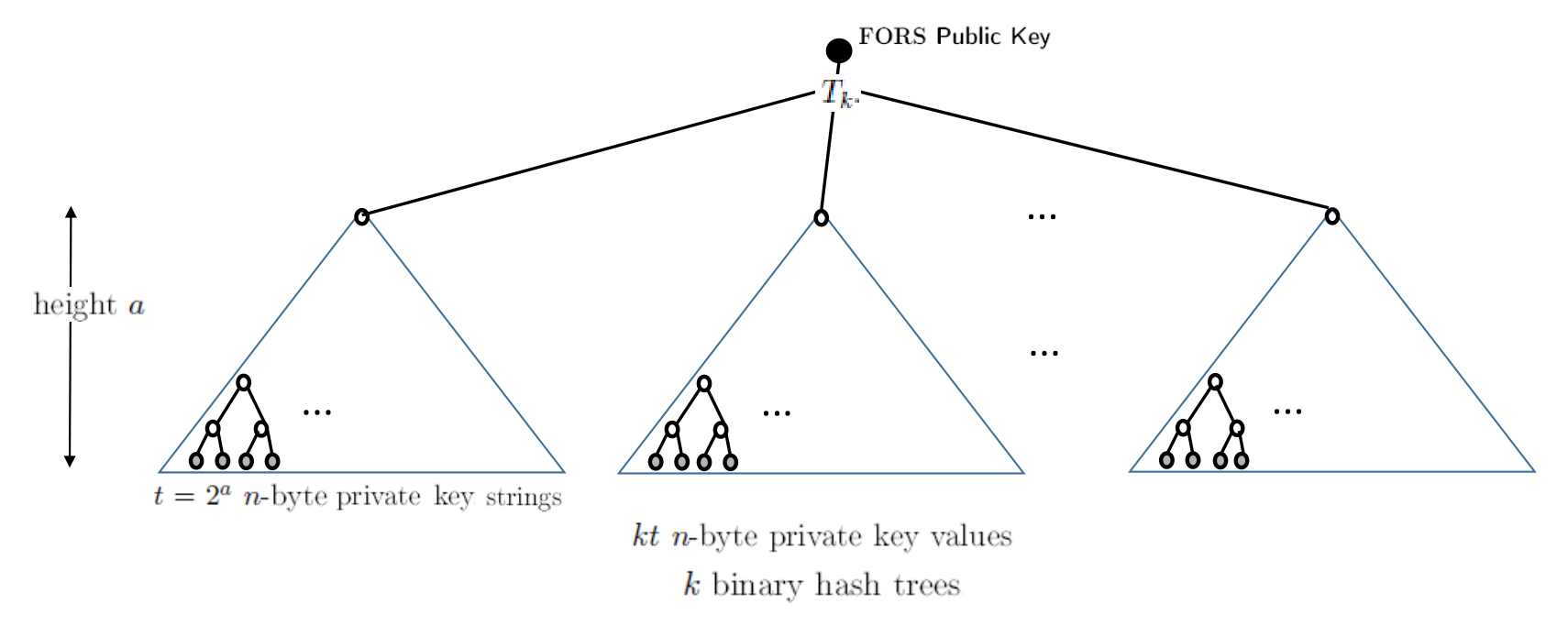
FTS node

Expanding this to use the parameters for SPHINCS+-SHA2-128f-simple, namely $h=66,\, d=22,\, k=33,\, t=2^6=64$, we have.

The hypertree (HT) subtree size is $h/d = 66/22 = 3$
- so each subtree has $2^3 = 8$ OTS nodes.
We have $d=22$ subtrees
- so we have $(2^3)^{22} = 2^{66}$ OTS nodes at the bottom HT layer
- each signing a FORS tree (FTS node)
Each FORS tree has $kt = 33 \cdot 2^6$ private key values
- giving a total number of private key values $= 33\cdot 2^6 \cdot 2^{66} \approx 2^{77}$
- this equals $1.56 \times 10^{23}$, about the number of stars in the Universe
Remember each of these private keys can be computed deterministically using SK.seed and the ADRS parameter. We don't have to create them all each time, and we only need a small subset when we create a signature.

Signature computations

When computing the signature values, the most important thing is to derive the correct ADRS parameter before calling the hash functions, F, H, etc. Note this well when following the calculations.

In the computations that follow, results that form part of the signature are shown

HIGHLIGHTED IN BLUE

<< previous: SPHINCS+ Introduction

Contents

next: Computing the FORS signature >>

Rate this page

Contact us

To comment on this page or to contact us, please send us a message.

This page first published 17 March 2023. Last updated 1 June 2024.