Computing the FORS signature

Compute the randomizer R
Compute H_msg
Split H_msg into message digest, tree address and leaf index
Compute the first FORS secret key
The first authentication path
Compute the remaining FORS signatures
Compressing the tree root values to form the FORS public key

We use JavaScript to display the mathematics on this page. Please enable JavaScript in your browser for it to work.

Step 1 - Compute the randomizer $R$

Compute the randomizer $R$ of $n$ bytes.

R = PRF_msg(SK.prf, OptRand, M)

where SK.prf is part of the private key, OptRand is a $n$-byte string initialized with zeros optionally overwritten with randomness, and M is the message to be signed.

Using SHA-256, PRF_msg is defined using HMAC-SHA-256 with SK.prf as the key.

PRF_msg(SK.prf, OptRand, M) = HMAC-SHA-256(SK.prf, OptRand || M) # truncated to 16 bytes

In this case, we have

SK.prf =2fd81a25ccb148032dcd739936737f2d
OptRand=33b3c07507e4201748494d832b6ee2a6
M=d81c4d8d734fcbfbeade3d3f8a039faa2a2c9957e835ad55b22e75bf57bb556ac8
hence R =

b77b5397031e67eb585dba86b10b710b

This is the first 16-byte line of the signature.

Note that this randomizer value $R$ is completely determined by the SPHINCS+ private key and the message itself, and perhaps some optional random material.

Python code

# Compute the randomizer R of 16 bytes using hex strings
sk_prf='2fd81a25ccb148032dcd739936737f2d'
optrand='33b3c07507e4201748494d832b6ee2a6'
msg= \
'D81C4D8D734FCBFBEADE3D3F8A039FAA2A2C9957E835AD55B22E75BF57BB556AC8'
R = HMAC_SHA256(sk_prf, optrand + msg)
R = R[:32] # Truncate to 16 bytes
print("R =", R)
# R = b77b5397031e67eb585dba86b10b710b

Step 2 - Compute `H_msg`

We compute H_msg from the message, M, the public key, and the randomizer, R.

With SHA-256 we use MGF1 from PKCS#1 as an XOF (eXtendable Output Function).

H_msg(R, PK.seed, PK.root, M)
  = MGF1-SHA-256(SHA-256(R||PK.seed||PK.root||M), m)

In our case, we require an output of $m=34$ bytes (see below).

Python code to compute $H_{\text{msg}}$

R = 'b77b5397031e67eb585dba86b10b710b'
PKseed = 'B505D7CFAD1B497499323C8686325E47'
PKroot = '4FDFA42840C84B1DDD0EA5CE46482020'
msg= \
'D81C4D8D734FCBFBEADE3D3F8A039FAA2A2C9957E835AD55B22E75BF57BB556AC8'
print("Input =", R + PKseed + PKroot + msg)
h = SHA256(R + PKseed + PKroot + msg)
print("h =", h)
# 3b5c056af3ebba70d4c805380420585562b32410a778f558ff951252407647e3
h_msg = MGF1_SHA256(h, 34)
print("H_msg:", h_msg)
# 5b7eb772aecf04c74af07d9d9c1c1f8d3a90dcda00d5bab1dc28daecdc86eb87611e

Note that the function to derive H_msg using SHA-256 has since been changed in SPHINCS+ version 3.1. These changes are not reflected here.

Split `H_msg` into message digest, tree address and leaf index

For our example, we have the following parameters

md length=25
SPX_FORS_HEIGHT=6 SPX_FORS_TREES=33
SPX_TREE_BITS=63 SPX_TREE_BYTES=8
SPX_LEAF_BITS=3 SPX_LEAF_BYTES=1
SPX_DGST_BYTES=34

We require 25 bytes for the message digest (mhash) and enough bytes for a 63-bit tree address (8 bytes) and a 3-bit leaf index (1 byte) making $m=34$.

Split H_msg into mhash (25 bytes), tree address (8 bytes) and leaf index (1 byte)

H_msg = 5b7eb772aecf04c74af07d9d9c1c1f8d3a90dcda00d5bab1dc 28daecdc86eb8761 1e
mhash = 5b7eb772aecf04c74af07d9d9c1c1f8d3a90dcda00d5bab1dc

Then decode the tree address and leaf index byte strings to unsigned integers truncated to 63 and 3 bits, respectively

treeaddr = 0x28daecdc86eb8761 & 0x7fffffffffffffff  # 63 bits
= 0x28daecdc86eb8761
idx_leaf = 0x1e & 0x7  # 3 bits
= 0x6

Interpret 25-byte mhash as 33 $\times$ 6-bit unsigned integers (with each byte of mhash interpreted in little-endian order).

mhash = 5b7eb772aecf04c74af07d9d9c1c1f8d3a90dcda00d5bab1dc
message_to_indices (in decimal):  
27 57 55 45 50 57 58 51 04 28 44 18 48 55 23 39
28 50 49 07 13 42 03 36 28 43 13 00 21 43 27 44
28

Each of these 33 indices gives the index (0-63) of a secret key in each of the 33 FORS trees. The first index (value 27) selects the 27th secret key in the 1st tree, the second (value 57) selects the 57th key in the 2nd tree, ... and finally the 33rd index (value 28) selects the 28th key in the 33rd tree.

Compute the first FORS secret key

NOTE: When using SHA-256, the ADRS parameter is compressed from 32 to 22 bytes (to minimise the number of calls to the compression function). So don't get too confused with the descriptions of the 32-byte hash function address scheme in section 2.7.3 of the specification.

In this case we construct an ADRS of type 3 for a FORS address. We are at layer 0, tree height 0, the leaf index (key pair address) is 6, and the index is 27.

The tree_index part of ADRS is computed as $it + \text{index}[i]$ for $i = 0\ldots 32$ and $t=64$. For the first key $i=0$ we have an index of 27 giving

tree_index = 0*64 + 27 = 27 = 0x1b

The full 22-byte ADRS_c structure is

layer   treeaddr  type  idxleaf  tree ht treeindex
[1]          [8]   [1]      [4]      [4]      [4]
00 28daecdc86eb8761 03 00000006 00000000 0000001b

The secret key value is computed using the PRF function:

sk = PRF(SK.seed, ADRS) = SHA256(SK.seed || ADRS_c)
   = SHA256(7c9935a0b07694aa0c6d10e4db6b1add
      + 0028daecdc86eb87610300000006000000000000001b)
   = 8c9f8091d1a1edbb6a8a041343c6e5c06cae46676fa62c2dea9158fb008ceb6c

Truncate the 32-byte output to the required $n=16$ giving the first secret key value in the signature.

8c9f8091d1a1edbb6a8a041343c6e5c0  # fors_sig_sk[0]

This is followed by the $6n$-byte FORS authentication path along the $a=6$ levels from the secret key to the FORS tree root. The path is computed using the TreeHash algorithm (more on this later).

90d9d26cf0068d14f2125ffa16dce594  # fors_auth_path[0]
3af75452a07b7bc67344a77fba2bc51f
1ee71cab80e5d588a4f3e181cfca703b
e987519c0578e6edc2cac80c3d0f5781
0d7dabe142fb0976638fe21d503dabde
606c9bbca50ee8112dcc0cea78e81501

The first authentication path

In the SPHINCS+ documentation and the reference implementation, the authentication path is computed using the TreeHash algorithm, which is based on the BDS algorithm [BDS08] and [KMN14]. There are other ways to do this, which we show in our Python code.

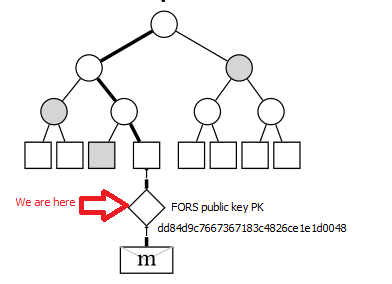
As an example, we can demonstrate how to start computing the authentication path for the first FORS tree where the index is 27. The diagram below shows the relevant part of the tree with the node hash values shortened to 3 bytes for brevity.

Part of FORS tree around index 27

The secret key values are

sk[24]=15ad2d3fd3e9cee4e03a26280097a3a7
sk[25]=ba1c9eb24ae495cf78522719633db5a8
sk[26]=f2a52fd5901fed2b171726739901a3f0
sk[27]=8c9f8091d1a1edbb6a8a041343c6e5c0  #fors_sig_sk[0]

The first value at treeHeight 0 on the authentication path is the leaf value of the secret key with index 26 (0x1a), the left sibling of the revealed secret key.

leaf_node = F(PK.seed, ADRS, sk) 
          = SHA256_t(BlockPad(PK.seed) || ADRS || sk)

where BlockPad pads the seed value from 16 bytes to 64 bytes with zeros^† and SHA256_t is the SHA-256 algorithm with its output truncated to the first $n=16$ bytes.

BlockPad(PK.seed)=B505D7CFAD1B497499323C8686325E47 \
00000000000000000000000000000000 \
00000000000000000000000000000000 \
00000000000000000000000000000000
ADRS=0028daecdc86eb87610300000006000000000000001a
leaf[26] = SHA256_t(B505D7CFAD1B497499323C8686325E47 \
       00000000000000000000000000000000 \
       00000000000000000000000000000000 \
       00000000000000000000000000000000
       + 0028daecdc86eb87610300000006000000000000001a
       + f2a52fd5901fed2b171726739901a3f0)
  = 90d9d26cf0068d14f2125ffa16dce594

† Using BlockPad to pad PK.seed to 64 bytes is used in the SHA-256 implementation to enable users to pre-compute the value and use it many times.

The second value at treeHeight 1 is the parent node of the leaf values for the secret keys with indices 24 and 25.

leaf[24]=cb5f2a23f2c72f0ad03ce325a70c0228
leaf[25]=2b1142e4c9db94e6e4be139f6520ae77
treeIndex = 25//2 = 12 = 0x0c
treeHeight = 1
ADRS=0028daecdc86eb87610300000006000000010000000c
                                       ^^      ^^
node = H(PK.seed, ADRS, node_left || node_right)
     = SHA256_t(BlockPad(PK.seed) 
       + 0028daecdc86eb87610300000006000000010000000c 
       + cb5f2a23f2c72f0ad03ce325a70c0228 
       + 2b1142e4c9db94e6e4be139f6520ae77
   = 3af75452a07b7bc67344a77fba2bc51f

This process is continued up the tree until we get the root value for this tree (8f5a82fe31bc814bdf198d01481651c5), which is not included in the signature, but is part of the compressed set of root values included to compute the FORS public key.

The authentication path is part of the signature:

90d9d26cf0068d14f2125ffa16dce594  # fors_auth_path[0]
3af75452a07b7bc67344a77fba2bc51f
1ee71cab80e5d588a4f3e181cfca703b
e987519c0578e6edc2cac80c3d0f5781
0d7dabe142fb0976638fe21d503dabde
606c9bbca50ee8112dcc0cea78e81501

Compute the remaining FORS signatures ($i=1\ldots 32$)

For the 2nd key ($i=1$) we have an index of 57 giving tree_index = 1*64 + 57 = 121 = 0x79 and the ADRS is updated to

ADRS_c = 0028daecdc86eb876103000000060000000000000079
sk = SHA256_t(7c9935a0b07694aa0c6d10e4db6b1add
       + 0028daecdc86eb876103000000060000000000000079)
   = 229f6db83fc861d6fc5877405f5b9466

Hence

229f6db83fc861d6fc5877405f5b9466  # fors_sig_sk[1]

and the authentication path (computed separately) is

f89299c474d12428ef8b71caaf1d0da0  # fors_auth_path[1]
c09b4ccd09b4e8094548a855ff8a1d5c
51bdf290db167d12bee212e246b1c9c3
09e01d922e09e0cbc6ace161266433d3
163bed69c47db1a4777877033433cb2d
903938edcd9718d81330ed6645316ce7

with tree root value 4ff05f5821b513a402be41ef4e76f81f (to be used to compute the FORS public key later)

This process is repeated for all $k$ of the trees giving 33 FORS signature value and authentication path sequences.

The 33rd and final FORS signature ($i=32$) is computed as follows

We have an index of 28 giving tree_index = 32*64 + 28 = 2076 = 0x81c

ADRS_c = 0028daecdc86eb87610300000006000000000000081c
sk = SHA256_t(7c9935a0b07694aa0c6d10e4db6b1add
       + 0028daecdc86eb87610300000006000000000000081c)
   = 446d9fc66808fcc5e0d47c0c381c7f9e

Hence

446d9fc66808fcc5e0d47c0c381c7f9e  # fors_sig_sk[32]

with authentication path

0d92eb3bc4a5220a39e5c834d1cced86  # fors_auth_path[32]
601a1ae606a87cc6919d4f1aca5744b6
341a0a87b9cf960cbb1cd800f5cb1738
683492ec5e1379ffb4f6117de296d7d0
d8f3158b367ccfdab8def4b2786f60d8
302f791fccc4ded35f988a70205be088

and root value for this tree b77027ab7c2815483900f93fa9e8335f.

Compressing the tree root values to form the FORS public key

We now have 33 $n$-byte root values for each of the $k=33$ trees. These are

roots=
8f5a82fe31bc814bdf198d01481651c5
4ff05f5821b513a402be41ef4e76f81f
e2f903edf67cc0e42491b60197ec3c8d
1c1f5ee2668ce176e2fc1cb3dd1955ae
8cc53ce4967de7a7d0f5801a05a3bc13
5abf39ff74988744a289cb5e4d24e450
ed83fcef7222b4d3b100f34903fcaa74
ffb073610569093493f14206c1474a60
e7dc4fbf58fea214f20e3b87b3b46654
dfd37050602d777dc7a0dc21a352087b
5ee4f4ac7ca0e6328f0d801bf8e86777
e0f1ea8dc77f0ebbbee42d7d83b93a9e
a8cdcde80f66c828f46cb8fa761c33e1
f78d9dc67de3b090ed26509b858cccb2
6a6ad79572962938f6d5cf1f4a65151c
30386715cb9c891067284d92d5a00016
1c69c83738bb830b0d13a83fe923adfd
21f5e3456a77cdb52a3a327a5824d39d
a3647dbd7879bfb66d91cbfb2c3532e0
84fb9617baf3f1cc299fdca8261e6d37
95536fa2d103aab2b967734ce2db9c65
3384e2eaff07cfbc363c4721d97a1b72
36b3c6b1d428944b74fc1a7245f55f65
da20b827e39bedbab25a5510b33f45ee
df3dd78d8d124daff7c237dd49ce92ff
547a0fd02fba955174be49c1c02580b9
84760d94a97bb2bc9f4f096ff4afe7a3
40c19b8da5272aa0cb53b60310e383b6
55144f23d2b3fc7a4254b5efe1cf8cf1
c2468e12d21908f85e844df5dd26e905
d16c2adc41a67ed5e8080b846cb5fce3
8f31d9a72dbe9584461d1efe3213dc60
b77027ab7c2815483900f93fa9e8335f

We don't save these tree root values explicitly - a verifier can recompute them using the revealed secret keys and the given authentication paths.

To compute the FORS public key, we use the T_k function to hash all these together with PK.seed and the ADRS parameter.

ADRS=0028daecdc86eb876104000000060000000000000000
FORS_PK = T_k(PK.seed, ADRS, roots)
        = SHA256_t(BlockPad(PK.seed) || ADRS || roots)
        = dd84d9c7667367183c4826ce1e1d0048

The FORS public key value (dd84d9c7667367183c4826ce1e1d0048) is not explicitly included in the signature, but is used as an input to the hypertree signature.

In the tree diagram above, we are now at the position shown. (Note that the location shown in this diagram does not match our real-life example.)

Location in tree

<< previous: SPHINCS+ Example

Contents

next: The Hyper Tree Signature (SIG_HT) >>

Rate this page

Contact us

To comment on this page or to contact us, please send us a message.

This page first published 17 March 2023. Last updated 9 September 2025.