 Chi-square formulae
Chi-square formulae
This page explains the formulae behind the $\chi^2$ (chi-square) distribution.
Suppose $X$ is a random variable having a $\chi^2$ (chi-square) distribution with $\nu$ degrees of freedom, then the p-value, $p$, for a given statistic $\chi^2$ is defined as $p=\Pr[X\geq \chi^2]$. The $p$-value is the area under the chi-square probability density function (pdf) curve to the right of the specified $\chi^2$ value.
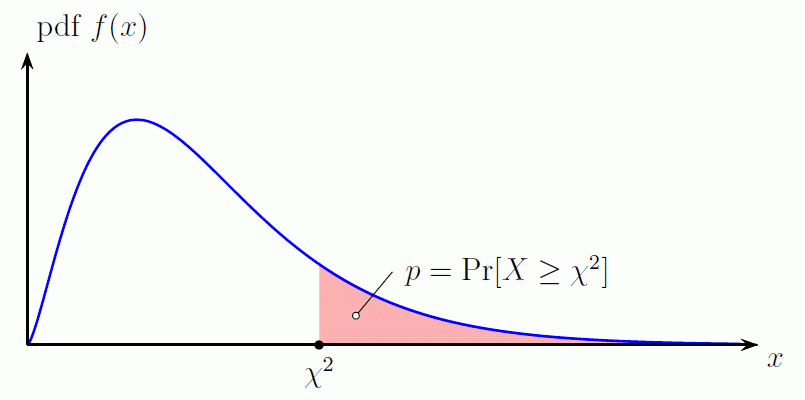
The value $p$ for a given $\chi^2$ is computed by putting $a = \nu/2$ and $x=\chi^2/2$ in the function $Q(a,x)$ given by \[ Q(a,x) = \frac{1}{\Gamma(a)}\int_x^\infty t^{a-1}e^{-t}\,dt \quad(a>0) \] and $\Gamma(a)$ is the gamma function defined by \[ \Gamma(a) = \int_0^\infty t^{a-1}e^{-t}\,dt \quad(a>0) \]
For integer values, $n\geq 0$, the gamma function becomes $\Gamma(n+1) = n!$, where $n!$ is the factorial function, $n! = 1\cdot 2\cdot 3\cdots (n-1)\cdot n$ with $0!=1$. The gamma function obeys a recurrence relation, $\Gamma(z+1) = z\Gamma(z)$.
Contact us
To comment on this page or to tell us about a mistake, please send us a message.
This page first published 13 January 2013. Last updated 9 September 2025.

